On December 1st, a paper titled Optical Trapping Separation of Chiral Nanoparticles by Subwavelength Slot Waveguides was published in Physical Review Letters by Professor Wang Jian’s group from Wuhan National Laboratory for Optoelectronics (WNLO), Huazhong University of Science and Technology. The paper proposed the chiral-separable optical trapping in the counter-propagating slot waveguides as a new chiral-selective silicon-based waveguide platform. These discovered waveguides may inspire a promising technology to exploit on-chip chiral optical tweezers or new optofluidic transport systems to obtain large-scale chiral separation.
Chirality, associated with the non-superimposable property of a structure with its mirror image, usually refers to an enantiomeric pair for chiral compounds in stereochemistry where the carbon atoms are aligned clockwise or counterclockwise. The concept of chirality has spread across numerous scientific disciplines, such as bioscience, biomedicine, physics, and even astronomy. The identification and separation of chiral materials may open substantial opportunities to promote their development within the chemical industry, biomedical technologies, food and environmental science and especially the research fields for pharmaceuticals and agrochemicals. However, currently the chiral analysis and separation still face great challenges, because the enantiomer pairs are almost identical in terms of chemical composition and physical properties. For example, the existing high-performance chiral liquid chromatography, as the most popular technique in chiral analysis, needs to add other chiral molecules interacting with each molecule in an enantiomeric pair. Unfortunately, these chemical processes may introduce unwanted side products resulting in bad ecological and economical effects.
In physical optics, the electromagnetic response to chiral materials manifests as the distinct chiral polarizabilities. Thanks to this property of light-matter interaction, it provides a potential to take a less invasive alternative to chemical methods for passively sorting enantiomers by exploiting chirality-dependent optical forces. In the past ten years, a variety of all-optical chiral resolution or separation schemes have been proposed. Compared with traditional technical solutions, the technology of all-optical chiral separation provides many advantages, such as being non-contact, low cost, unmixed with other matters, and easy to automatically manage.
Recently, the Multi-Dimensional Photonics Laboratory (MDPL) group led by Professor Wang Jian from WNLO, discovered and proposed a new all-optical chiral separation scheme, which exploits the counter-propagating sub-wavelength slot waveguides to trap and separate the chiral nanoparticles, as shown in Fig. 1. This chiral-separable silicon-based waveguide platform may provide some remarkable advantages over the current technical schemes. On the one hand, it could offer a higher feasibility for chiral separation by using the considerable gradient forces than the relatively weak nonconservative lateral forces induced by the transverse SAM. On the other hand, it enables nanometerscale enantiomer separation by the strongly confined gradient fields with relative low light power, beyond the free-space trapping systems when trapping nanoparticles due to the diffraction limit. More importantly, these silicon-based dielectric slot waveguides are completely compatible with the current mature silicon photonic integrated circuits and complementary metal oxide semiconductor technologies. Therefore, it can be easily developed into new optofluidic transport systems to realize large-scale chiral separation.
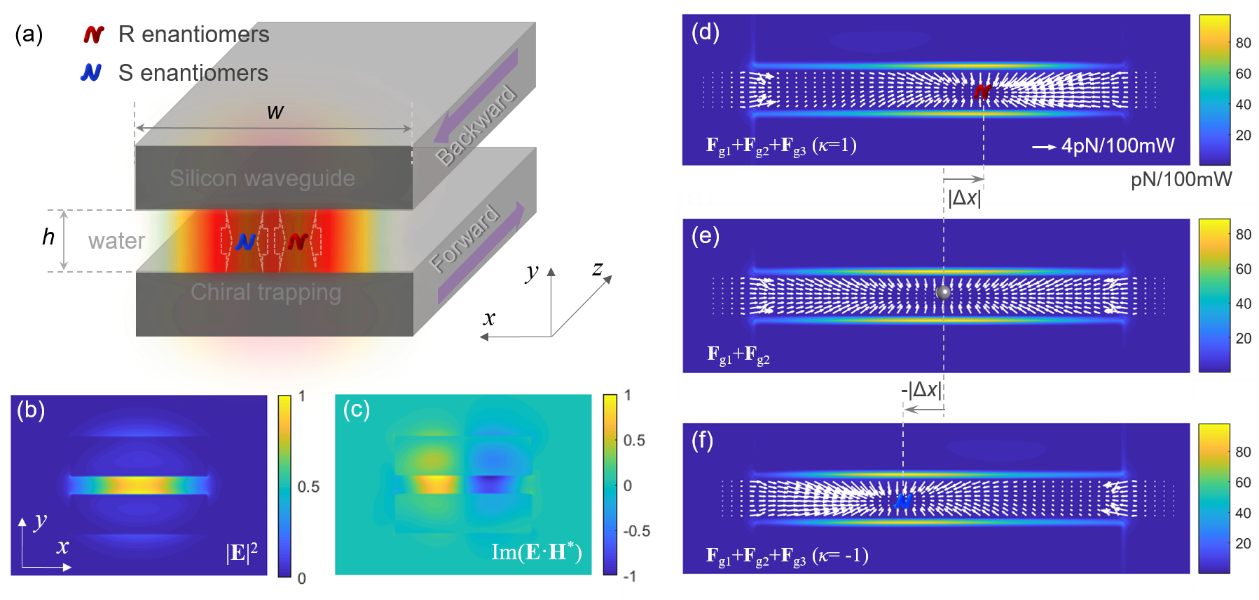
Fig. 1. Optical trapping separation in the counter-propagating slot waveguides. (a) Schematic of chiral trapping by the strongly confined standing evanescent fields in the gap of slot waveguides. (b) The electric-field intensity and (c) the imaginary part of electromagnetic product (chirality) of the PTM modes. The resulting trapping force potentials and chiral-dependent trapping shifts in the gap of slot waveguides for (d) R enantiomers, (e) achiral particles, and (f) S enantiomers.
The results obtained show that the trapping separation is largely determined by the width of the slot waveguide, as shown in Fig. 2, where the slot distance is h=100 nm. Especially, there is a specific transitional width of about w=0.6 μm, where the trapping equilibrium positions for R and S enantiomers would superpose in the center of the slot waveguides, and then exchange across this transitional width. Returning to the electromagnetic chirality as the foundation of the chiral-separable trapping, the group presents the electric-field and magnetic-field distributions, and the resulting imaginary part of electromagnetic product (chirality) of the PTM modes around this specific width. In particular, the evolution of magnetic-field distributions in the slot waveguides around this transitional width is depicted in Figs. 2(a)-2(d). From them, the magnetic-field circulations would split into two parts when enlarging the waveguide width over 0.6 μm. The chiral gradient forces Fg3 around this specific width for R enantiomers are further calculated, as shown in Fig. 2(f), as well as the resulting trapping forces in Fig. 2(g). Remarkably, it is the large circulation (slow variation) of magnetic fields for the waveguide width of about w= 0.6 μm shown in Fig. 2(b) that leads to the low gradient of electromagnetic chirality. Consequently, it gives rise to the weak gradient force Fg3 (green line) in Fig. 2(f) that the transitional position of the resulting force Fg (green line) appears in the center of the slot, relative to other width values in Fig. 2(g). Additionally, the trapping forces Fg versus varied slot distances are calculated and plotted in Fig. 2(h). From Figs. 2(g) and 2(h), it shows that the trapping forces become weaker and weaker when gradually enlarging (broadening or opening) the slot space between two waveguides.
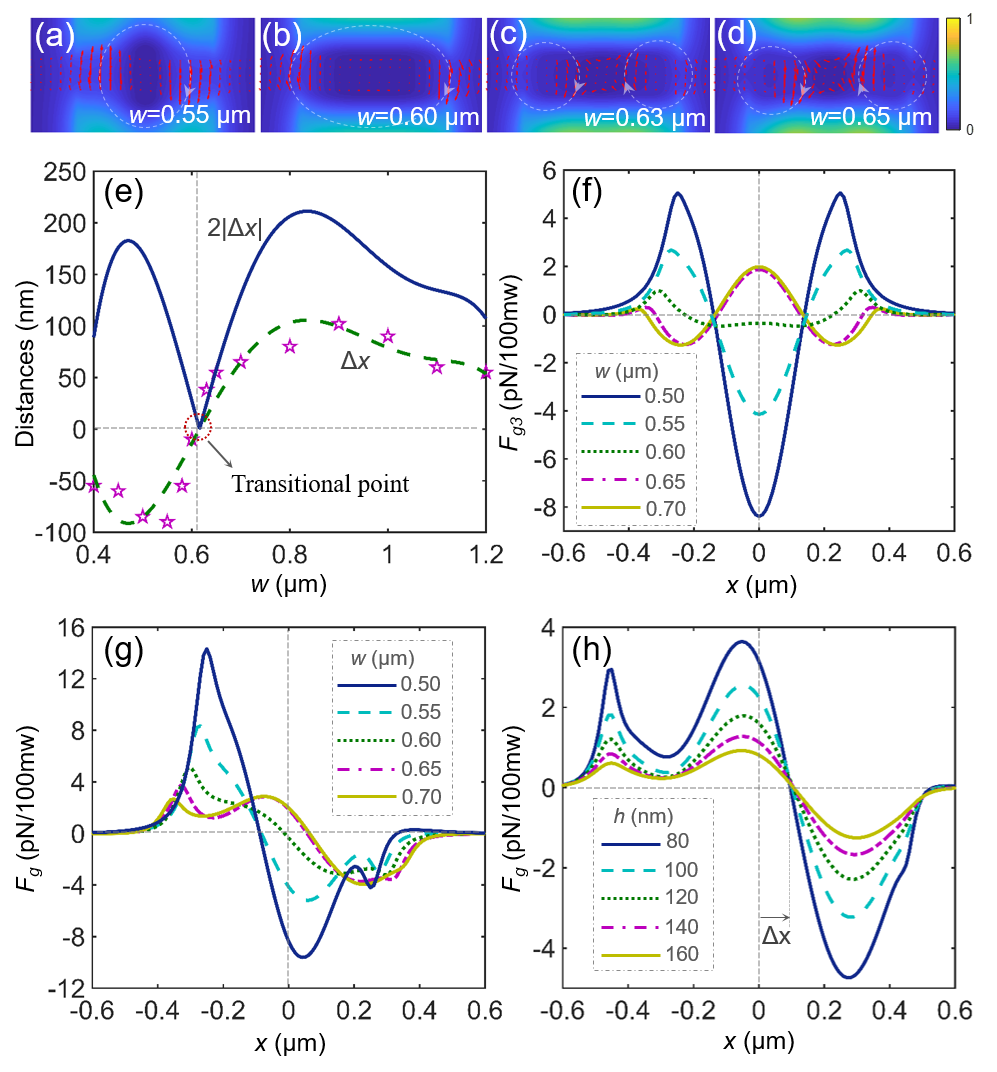
Fig. 2. Magnetic-field distributions, chiral-dependent gradient forces, or trapping separation for the R enantiomers (κ=1) with the radius of 12 nm under varied parameters of the slot waveguides in the wavelength of 1550 nm. (a)-(d) The magnetic-field distributions in the slot waveguides with a slot distance h=100 nm and different widths. (e) The degrees of trapping separation versus widths varied from 0.4 μm to 1.2 μm. Note that the stars denote the discrete simulation data, and the curves indicate fitted values. (f) The chiral gradient forces Fg3, and (g) the resulting trapping forces Fg under different widths, when h =100 nm. (h) The resulting forces Fg under different slot distances, when w =0.9 μm.
For the chiral nanoparticles, it is convenient and precise enough to employ the non-inertial approximation (negligible mass) of Langevin dynamics approach to simulate the chiral-separable driving motion. The simulation results show that the positions of trapping separation in the end of the trajectories for three kinds of nanoparticles in Fig. 3 are completely in accord with the calculation results in Fig. 1. Furthermore, the chiral-distinguishable investigation results show that for the size of a=12 nm, the smallest chiral-distinguishable power is about a few milliwatts; while for the input power of 100 mW, the smallest chiral-distinguishable size is about a=2 nm, as shown in Fig. 4. All the obtained results demonstrate that the chiral-dependent gradient forces can overcome both the friction forces and thermal forces to achieve the chiral separation by the counter-propagating slot waveguides proposed here.
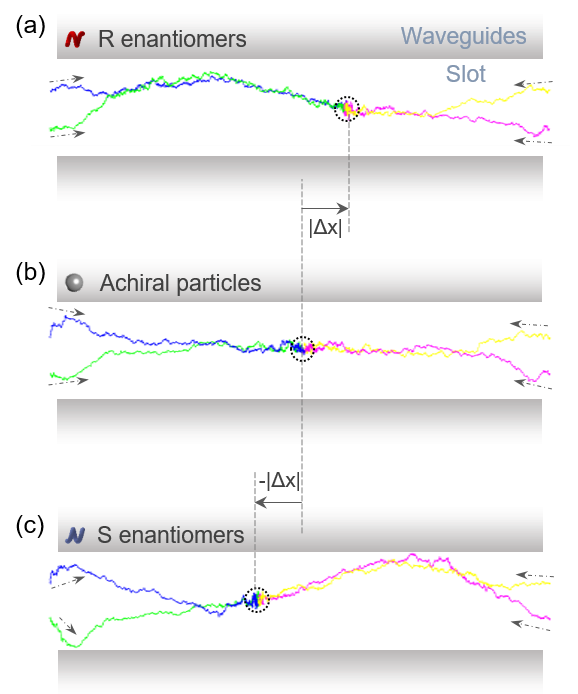
Fig. 3. 2D stochastic Brownian motion simulation of chiral-selective driving and trapping in the slot waveguides for (a) R enantiomers, (b) achiral particles, and (c) S enantiomers. Note that the lines marked with different colors represent the trajectories of moving particles from different initial positions.

Fig. 4. 2D stochastic Brownian motion simulation of chiral-selective driving and trapping in the waveguide slot. When the input power of light is (a) P=100 mW, (b) P=10 mW, and (c) P=1 mW, respectively, while the size of chiral nanoparticles is a=12.0 nm. When the sizes of chiral nanoparticles are (d) a=6.0 nm, (e) a=2.0 nm, and (f) a=1.0nm, while the input power is P=100 mW, respectively. Note that the three color lines represent the motion trajectories of three kinds of nanoparticles.
Fang Liang, a postdoctoral fellow from WNLO, is the first author of this paper, and Professor Wang Jian is the corresponding author.
Paper link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.233902
Written by: Wang Jian, Fang Liang, Gou Bingbing
Reviewed by: Andrew, Peng Yumeng